|
𝔾𝕣𝕒𝕗𝕚𝕔𝕠𝕤 𝕕𝕖 𝔼𝔻𝕆𝕤
Alguns gráficos interessantes que eu obtive enquanto estudava EDO's e seus métodos numéricos. 𝕀𝕟𝕕𝕚𝕔𝕖 ⟼ Método de Euler ⟼ Aumento profressivo do $n$ ⟼ Método de Picard
𝕄𝕖𝕥𝕠𝕕𝕠 𝕕𝕖 𝔼𝕦𝕝𝕖𝕣 (topo)
Aqui vão alguns gráficos de equações diferenciais ordinárias que eu fiz com uma implementação do método de Euler em Python, plotados usando matplotlib. Cada linha é a aproximação da solução da EDO em uma condição inicial diferente. Aqui os domínios foram discretizados em 10'000 pontos, e foram tomadas condições iniciais com 0.05 de diferença entre elas. $$\dot{y} = y(1-y)$$ .png)
Esse é um exemplo que o professor passou em classe. Essa EDO tem $y=0$ e $y=1$ como pontos de estabilidade, mas $y=0$ é um ponto expulsor (soluções próximas se afastam), enquanto $y=1$ é um ponto atrator (soluções próximas se aproximam). $$\dot{y} = y^2(1-y)$$ .png)
Essa é parecida, mas o ponto de baixo agora é atrator para soluções abaixo dele e repulsor para soluções acima. Bem estranho. $$\dot{y} = y(1-y^2)$$ .png)
Aqui o ponto $x=0$ é um repulsor, enquanto $y=1$ e $y=-1$ são atratores. $$\dot{y} = \sin(t) \cdot y$$ y.png)
Nesse, o $y=0$ é estável, mas não existem atratores nem repulsores. $$\dot{y} = \tan(t) \cdot y$$ y.png)
Parecido com o anterior, mas com um comportamento assintótico em alguns pontos periódicamente (por conta do comportamento semelhante da tangente). Esse gráfico só aparece assim pois o domínio é discretizado, então os pontos em que a solução diverge para o infinito são pulados. Na realidade, o intervalo de solução deve ser escolhido dentre um desses intervalos do tipo $(\pi/2 + 2k\pi, 2\pi/3 + 2k\pi)$. Mas, não deixa de ser maneiro :)
𝔸𝕦𝕞𝕖𝕟𝕥𝕠 𝕡𝕣𝕠𝕘𝕣𝕖𝕤𝕤𝕚𝕧𝕠 𝕕𝕠 $n$ (topo)
Aqui tomamos uma condição inicial fixa e então progressivamente aumentamos o número de pontos. Os resultados são comparados com a respectiva aproximação com 10'000 pontos, cuja diferença pra solução exata é desprezível. $$\begin{cases} \dot{y} = y(1-y) \\ y_0 = 0.5 \end{cases}$$ 0p5.gif)
$$\begin{cases} \dot{y} = y(1-y) \\ y_0 = 1.5 \end{cases}$$ 1p5.gif)
$$\begin{cases} \dot{y} = y(1-y) \\ y_0 = -0.1 \end{cases}$$ m0p1.gif)
Aqui podemos ver uma dificuldade maior quando a variação da curva integral é muito grande. $$\begin{cases} \dot{y} = \sin(t) \cdot y \\ y_0 = 1 \end{cases}$$ 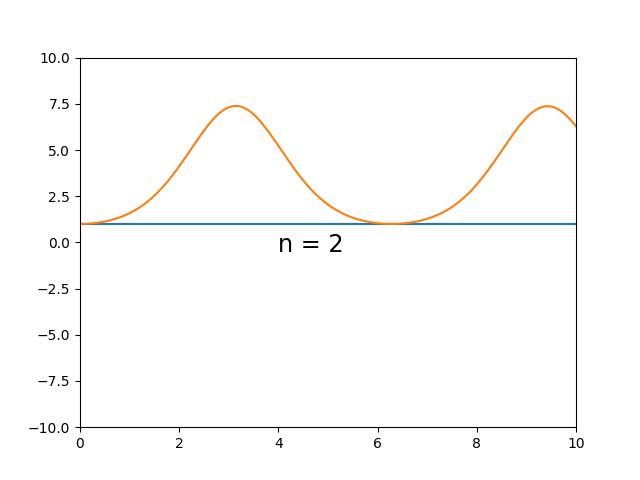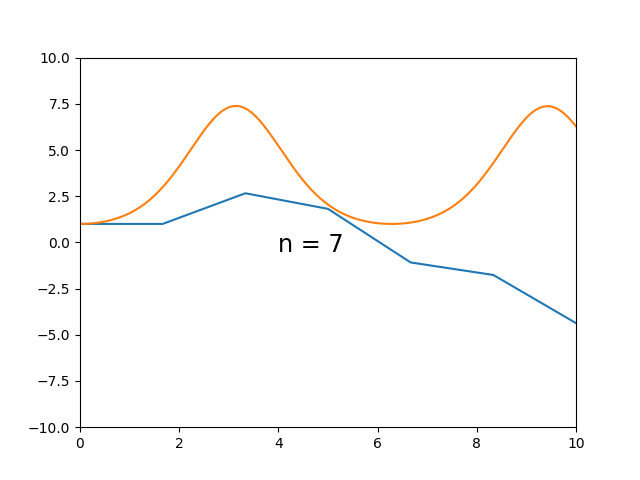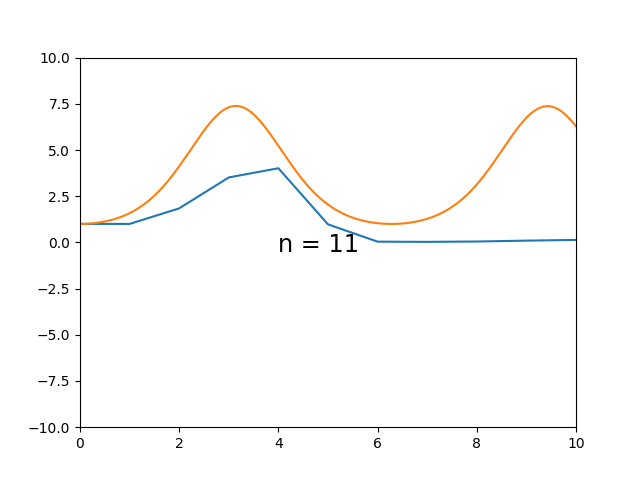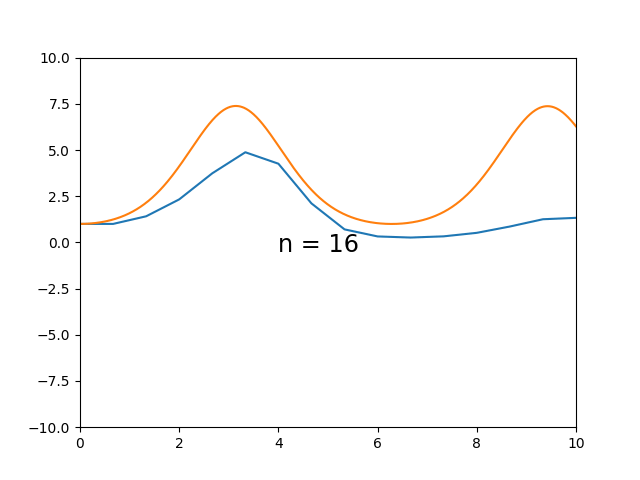
Aqui podemos notar que o método apresenta dificuldade em casos de mudança no sinal da derivada da solução exata, i.e. a curva integral sobe e então desce. Pode-se observar que o método é capaz de aproximar razoavelmente o início monotônico da curva, mas logo se torna muito impreciso. $$\begin{cases} \dot{y} = \tan(t) \cdot y \\ y_0 = 1 \end{cases}$$ 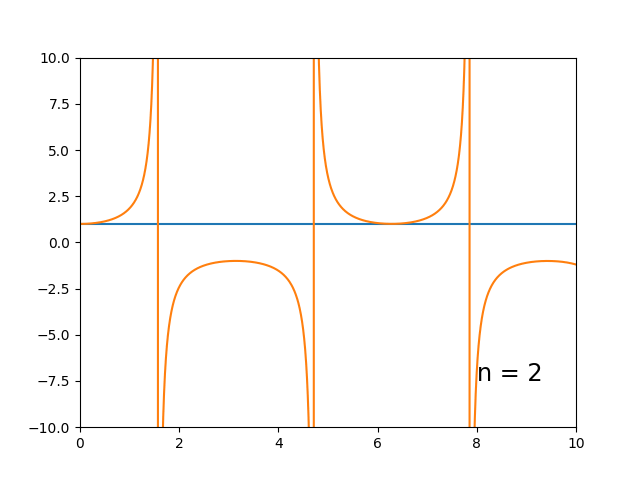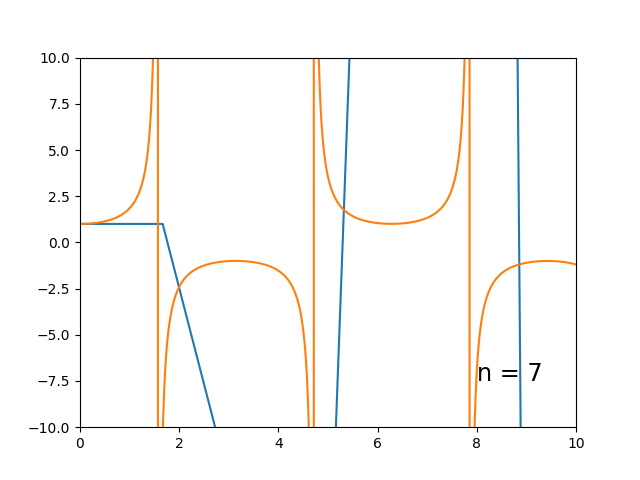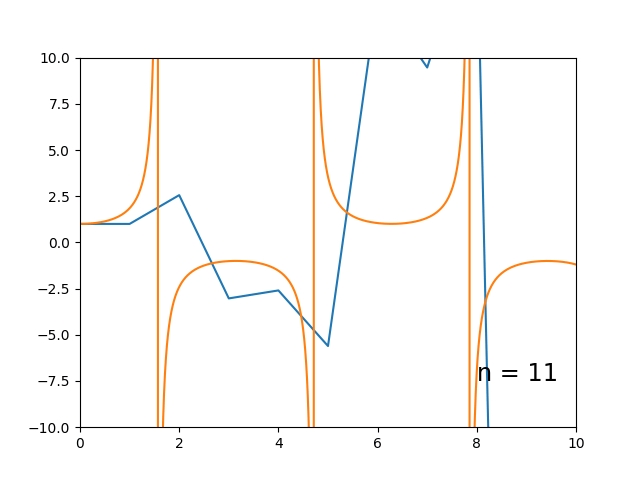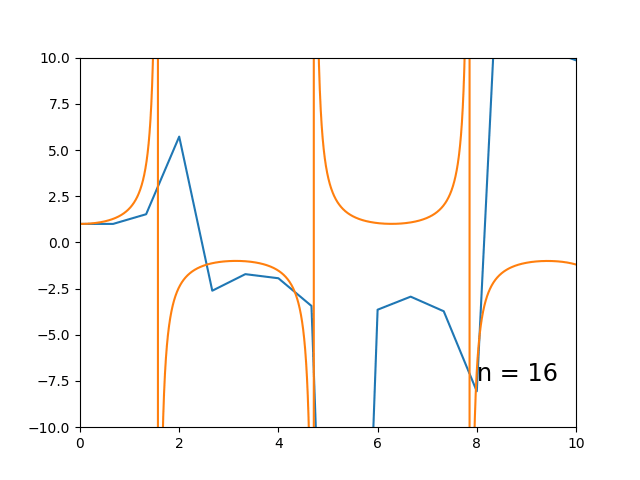
Esse eu fiz mais pela brincadeira, mas dá pra ver o mesmo princípio em ação: o começo (monotônico) da curva integral é bem representado, mas depois vai pro escambau. É importante notar aqui que as aproximações obtidas são ruins apenas pela ordem muito baixa do número de pontos. Na realidade, é bastante impressionante o quão preciso um método dessa simplicidade pode se tornar, se escolhermos uma partição suficientemente fina.
𝕄𝕖𝕥𝕠𝕕𝕠 𝕕𝕖 ℙ𝕚𝕔𝕒𝕣𝕕 (topo)
Tomando a EDO $\dot{y} = t \cdot y \cdot (1-y)$, utilizei o método de integração numérica do SAGE para aplicar sucessivamente o Método de Picard (nota, wiki), obtendo aproximações sucessivas da solução para a condição inicial $y(0) = 0.2$. Primeiro, no terminal do SAGE, importamos os métodos de integração simbólica e definimos $f$, $y_0$ e $t_0$: sage: from sage.symbolic.integration.integral import * sage: f(t,y) = t*y*(1-y) sage: y0 = 1/5 sage: t0 = 0 e então, definimos a primeira aproximação $\varphi_0 = y_0$ e melhoramos a aproximação conforme o método. sage: F(t) = y0 sage: F(t) = y0 + definite_integral(f(x, F(x)), x, t0, t) sage: F t |--> 2/25*t^2 + 1/5 Uma vez que $f$ é uma função polinomial, todas as aproximações são polinômios e, como a integração de polinômios é simples, podemos aplicar o método quantas vezes quisermos. Então, basta plotar! A aproximação exata por método de Euler da EDO nessa condição inicial é 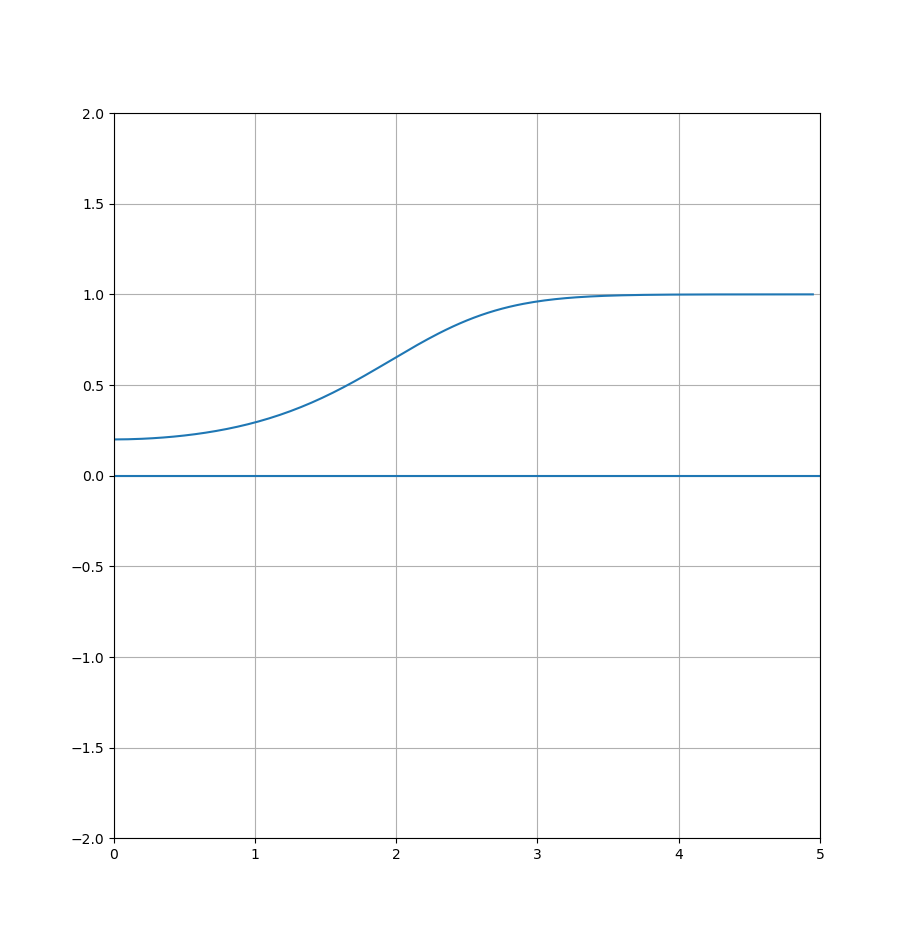
Cada aproximação sucessiva do método nos rende 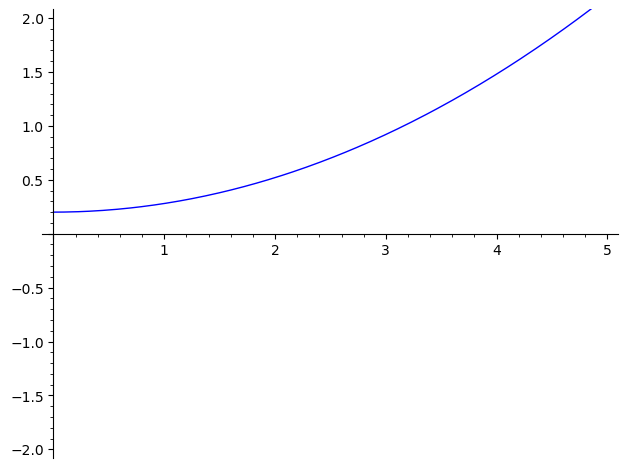
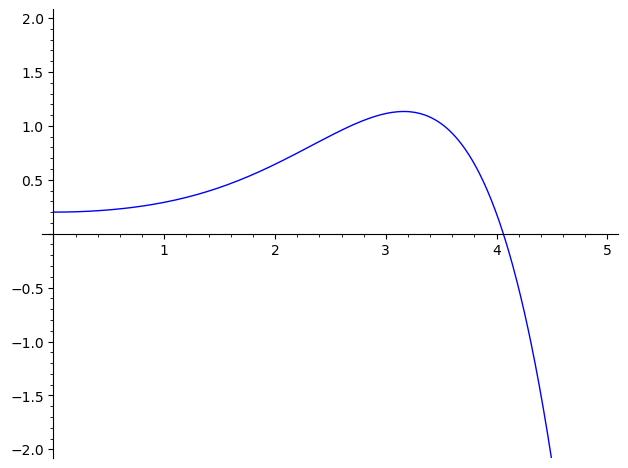
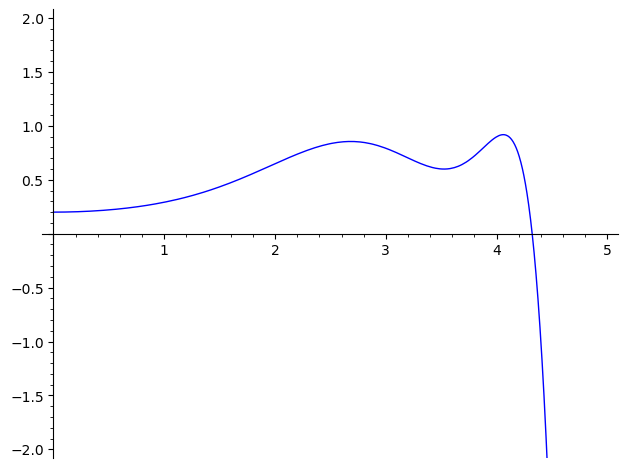
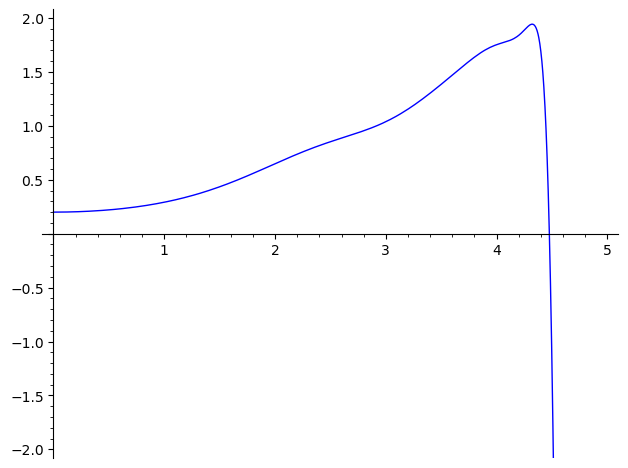
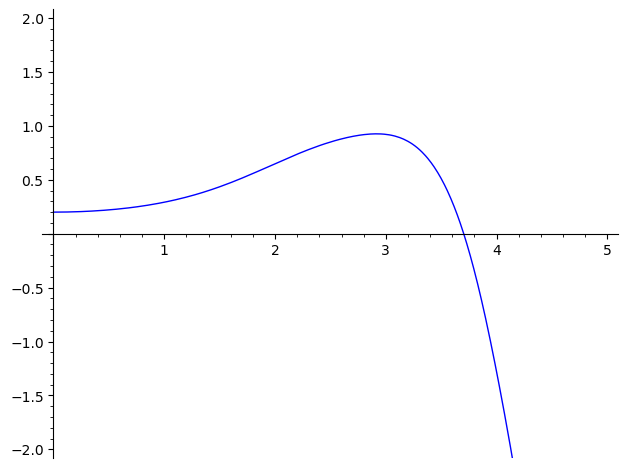
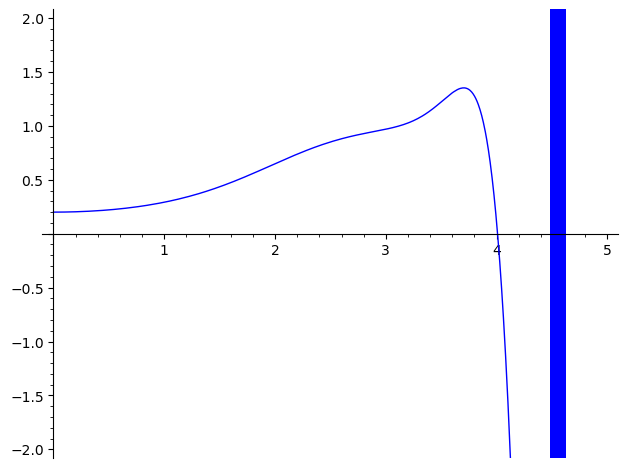
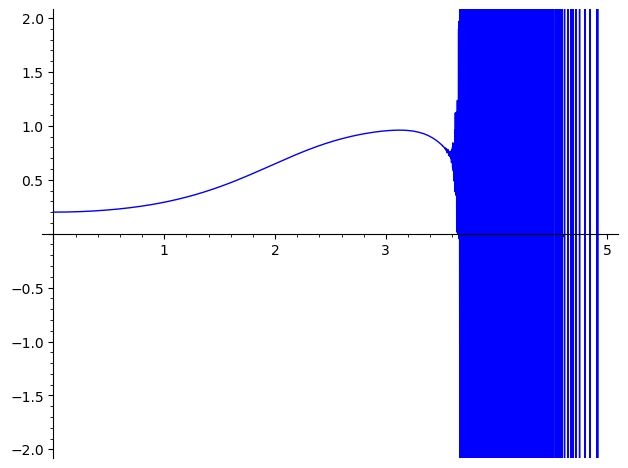
Sinceramente, esses resultados são interessantes mas... não muito impressionates! Eles exemplificam como o método de Picard tem seu valor analítico, mas simplesmente não rende aproximações boas o suficiente para uma EDO minimamente complicada. Outro detalhe é a natureza exponencial do grau desses polinômios. Nós começamos com um polinômio de grau 2, como mostrado acima, e esse grau rapidamente dispara: $$ \begin{align*} \text{deg}(\varphi_1) &= 2 \\ \text{deg}(\varphi_2) &= 6 \\ \text{deg}(\varphi_3) &= 14 \\ \text{deg}(\varphi_4) &= 30 \\ \text{deg}(\varphi_5) &= 62 \\ \text{deg}(\varphi_6) &= 126 \\ \end{align*} $$As próximas já teriam grau 254, e então 510. O SAGE já se recusa a plotar a sétima aproximação, pois não consegue calcular $\varphi_7(5)$ (e certamente a aproximação ainda não está nem próxima do que temos com o Euler!) A título de curiosidade, a oitava aproximação (com coeficientes em ponto flutuante) já é:
t |--> -(2.76977619902126e-565)*t^1022 + (5.30758364137449e-562)*t^1020 - (4.99920355614344e-559)*t^1018 + (3.08391186562863e-556)*t^1016 - (1.40065189738511e-553)*t^1014 + (4.99180649277594e-551)*t^1012 - (1.45283661944769e-548)*t^1010 + (3.54811615001673e-546)*t^1008 - (7.41403934269439e-544)*t^1006 + (1.34479907713511e-541)*t^1004 - (2.14064797503106e-539)*t^1002 + (3.01523662193202e-537)*t^1000 - (3.78174211529746e-535)*t^998 + (4.24235881960470e-533)*t^996 - (4.26904890602524e-531)*t^994 + (3.85869616442235e-529)*t^992 - (3.13149340971571e-527)*t^990 + (2.27576242008941e-525)*t^988 - (1.47257795829474e-523)*t^986 + (8.39312659854197e-522)*t^984 - (4.12885046731621e-520)*t^982 + (1.68008472888199e-518)*t^980 - (5.04646215751332e-517)*t^978 + (5.92379455067414e-516)*t^976 + (5.00747007010704e-514)*t^974 - (4.51672831853764e-512)*t^972 + (2.15238032819669e-510)*t^970 - (6.38072027422932e-509)*t^968 + (5.50605367889056e-508)*t^966 + (6.29954254003604e-506)*t^964 - (4.34411671986226e-504)*t^962 + (1.48675327238370e-502)*t^960 - (1.98001969336009e-501)*t^958 - (9.17108953180628e-500)*t^956 + (6.93747717767042e-498)*t^954 - (2.16289057066823e-496)*t^952 + (1.76167755529856e-495)*t^950 + (1.66670763311734e-493)*t^948 - (9.04265930458588e-492)*t^946 + (1.96920310833854e-490)*t^944 + (1.42794411704294e-489)*t^942 - (2.52716587706161e-487)*t^940 + (8.14840949955861e-486)*t^938 - (5.94718750656209e-485)*t^936 - (5.38459904520635e-483)*t^934 + (2.39584490208156e-481)*t^932 - (3.35903809868112e-480)*t^930 - (9.38560236796952e-479)*t^928 + (5.77201161149427e-477)*t^926 - (1.02933519753491e-475)*t^924 - (1.44828942208441e-474)*t^922 + (1.21792261022134e-472)*t^920 - (2.39637817464032e-471)*t^918 - (2.26178786367143e-470)*t^916 + (2.33437286766829e-468)*t^914 - (4.59871297837758e-467)*t^912 - (4.13099377023233e-466)*t^910 + (4.12691246139437e-464)*t^908 - (7.43329974734135e-463)*t^906 - (8.69452731202287e-462)*t^904 + (6.71341924849642e-460)*t^902 - (9.97985522190185e-459)*t^900 - (1.82844831634764e-457)*t^898 + (9.88867661438432e-456)*t^896 - (1.04190137759738e-454)*t^894 - (3.46255155670214e-453)*t^892 + (1.28377764726057e-451)*t^890 - (6.47688629528137e-451)*t^888 - (5.64461154854711e-449)*t^886 + (1.40905718907624e-447)*t^884 + (3.19899559635991e-447)*t^882 - (7.74486283382763e-445)*t^880 + (1.20665314725989e-443)*t^878 + (1.72202255507564e-442)*t^876 - (8.72506210315028e-441)*t^874 + (6.20285175527726e-440)*t^872 + (3.07128373913091e-438)*t^870 - (7.67952208522475e-437)*t^868 - (2.04621797062258e-436)*t^866 + (3.71800772534090e-434)*t^864 - (4.57238575149424e-433)*t^862 - (9.42246370488685e-432)*t^860 + (3.26082508928829e-430)*t^858 - (5.49889248349756e-430)*t^856 - (1.26580596754005e-427)*t^854 + (1.88492185615338e-426)*t^852 + (2.62790936983889e-425)*t^850 - (1.07074230899176e-423)*t^848 + (2.96079588706119e-423)*t^846 + (3.73447964527051e-421)*t^844 - (5.49647710693238e-420)*t^842 - (7.56721068594872e-419)*t^840 + (2.86250611630747e-417)*t^838 - (4.02830033945619e-417)*t^836 - (9.77837932631774e-415)*t^834 + (1.16635107830428e-413)*t^832 + (2.20281382674821e-412)*t^830 - (6.20610106509083e-411)*t^828 - (1.38594016499006e-410)*t^826 + (2.20799113477686e-408)*t^824 - (1.60676885351460e-407)*t^822 - (5.73482978273196e-406)*t^820 + (1.03000208505938e-404)*t^818 + (9.27148886436068e-404)*t^816 - (4.03156866565031e-402)*t^814 + (4.76447562422817e-402)*t^812 + (1.20030539222530e-399)*t^810 - (1.09943930820042e-398)*t^808 - (2.75104708174302e-397)*t^806 + (5.35288501271473e-396)*t^804 + (4.11149529383668e-395)*t^802 - (1.85221090486160e-393)*t^800 + (1.28030312486400e-393)*t^798 + (5.17448081155615e-391)*t^796 - (3.84536587062435e-390)*t^794 - (1.18618902404033e-388)*t^792 + (1.81921303577175e-387)*t^790 + (2.09089619741095e-386)*t^788 - (6.17940729772852e-385)*t^786 - (1.89468493194681e-384)*t^784 + (1.74139381739669e-382)*t^782 - (4.91561867978841e-382)*t^780 - (4.23360331910080e-380)*t^778 + (3.53845035119984e-379)*t^776 + (8.88070620318657e-378)*t^774 - (1.34257338218204e-376)*t^772 - (1.54028609848640e-375)*t^770 + (4.05365794276104e-374)*t^768 + (1.84471621783814e-373)*t^766 - (1.06431041025742e-371)*t^764 + (3.39855537538996e-372)*t^762 + (2.50925930389965e-369)*t^760 - (1.14015810066941e-368)*t^758 - (5.37323266679675e-367)*t^756 + (4.77413256407083e-366)*t^754 + (1.04322677611682e-364)*t^752 - (1.47397536001583e-363)*t^750 - (1.80400841971862e-362)*t^748 + (3.91869019794650e-361)*t^746 + (2.63363398316367e-360)*t^744 - (9.44363484712952e-359)*t^742 - (2.66562203219815e-358)*t^740 + (2.11225011210158e-356)*t^738 - (6.92863942778829e-357)*t^736 - (4.44122689400071e-354)*t^734 + (1.39622056139567e-353)*t^732 + (8.84369901597111e-352)*t^730 - (5.19544887260821e-351)*t^728 - (1.67489190765464e-349)*t^726 + (1.46024097587453e-348)*t^724 + (3.02291309853559e-347)*t^722 - (3.59066893055946e-346)*t^720 - (5.19915407016237e-345)*t^718 + (8.11910026370276e-344)*t^716 + (8.50124893358385e-343)*t^714 - (1.72848458825699e-341)*t^712 - (1.31404550939767e-340)*t^710 + (3.51139490922559e-339)*t^708 + (1.89822735848592e-338)*t^706 - (6.86595954414070e-337)*t^704 - (2.50307819064397e-336)*t^702 + (1.30006737945638e-334)*t^700 + (2.84922548275107e-334)*t^698 - (2.39471024855497e-332)*t^696 - (2.31887997535579e-332)*t^694 + (4.30650580957217e-330)*t^692 - (2.97177754718843e-331)*t^690 - (7.58332373795938e-328)*t^688 + (7.18014183585634e-328)*t^686 + (1.31076211424263e-325)*t^684 - (2.20201761003680e-325)*t^682 - (2.22851869629874e-323)*t^680 + (5.07168118273701e-323)*t^678 + (3.73325634218866e-321)*t^676 - (1.02193587614917e-320)*t^674 - (6.17094126526026e-319)*t^672 + (1.89161588241782e-318)*t^670 + (1.00759148962191e-316)*t^668 - (3.28451971654700e-316)*t^666 - (1.62640451743308e-314)*t^664 + (5.40172033377819e-314)*t^662 + (2.59650410206232e-312)*t^660 - (8.44357120714407e-312)*t^658 - (4.10049889667327e-310)*t^656 + (1.25292033170852e-309)*t^654 + (6.40490439267345e-308)*t^652 - (1.75348463365159e-307)*t^650 - (9.89089103404298e-306)*t^648 + (2.28010677017056e-305)*t^646 + (1.50907287637236e-303)*t^644 - (2.66406315036656e-303)*t^642 - (2.27267888208584e-301)*t^640 + (2.55604645205565e-301)*t^638 + (3.37460436947658e-299)*t^636 - (1.30989043261118e-299)*t^634 - (4.93371040528760e-297)*t^632 - (2.18173042135417e-297)*t^630 + (7.09087413006759e-295)*t^628 + (9.70584961949812e-295)*t^626 - (9.99988574032287e-293)*t^624 - (2.40000103273793e-292)*t^622 + (1.38072155680525e-290)*t^620 + (4.90580905243030e-290)*t^618 - (1.86155844321285e-288)*t^616 - (9.04297983579733e-288)*t^614 + (2.44259797966872e-286)*t^612 + (1.55438708299815e-285)*t^610 - (3.10536803861323e-284)*t^608 - (2.53201875309684e-283)*t^606 + (3.80167386924225e-282)*t^604 + (3.94289636690636e-281)*t^602 - (4.44010012614122e-280)*t^600 - (5.89827967514752e-279)*t^598 + (4.87146794564705e-278)*t^596 + (8.49834578446952e-277)*t^594 - (4.87576991081035e-276)*t^592 - (1.18061612264941e-274)*t^590 + (4.15455126086408e-274)*t^588 + (1.58116197440403e-272)*t^586 - (2.33412480129855e-272)*t^584 - (2.03867058616633e-270)*t^582 - (1.01402265568735e-270)*t^580 + (2.52364433155424e-268)*t^578 + (6.32933274734575e-268)*t^576 - (2.98536949809027e-266)*t^574 - (1.39902331503953e-265)*t^572 + (3.34900451240497e-264)*t^570 + (2.42136085180674e-263)*t^568 - (3.51583332371965e-262)*t^566 - (3.69316819946915e-261)*t^564 + (3.36836500225423e-260)*t^562 + (5.16610322305219e-259)*t^560 - (2.78171892932411e-258)*t^558 - (6.73881967477442e-257)*t^556 + (1.64199085469828e-256)*t^554 + (8.25048777219201e-255)*t^552 + (1.29014122149135e-255)*t^550 - (9.48301852839974e-253)*t^548 - (2.54509832937051e-252)*t^546 + (1.01754311972372e-250)*t^544 + (5.52749678750863e-250)*t^542 - (1.00524759843002e-248)*t^540 - (8.88350148722295e-248)*t^538 + (8.86716531770108e-247)*t^536 + (1.22991976622356e-245)*t^534 - (6.45345063665919e-245)*t^532 - (1.53532070452565e-243)*t^530 + (2.78143954096681e-243)*t^528 + (1.75559940413829e-241)*t^526 + (1.99583986828573e-241)*t^524 - (1.84149143850714e-239)*t^522 - (7.51695453555437e-239)*t^520 + (1.75192049602856e-237)*t^518 + (1.32199020825021e-236)*t^516 - (1.46325892599000e-235)*t^514 - (1.83912083767417e-234)*t^512 + (9.77569934246390e-234)*t^510 + (2.22568532028058e-232)*t^508 - (3.27791392912175e-232)*t^506 - (2.41059332261868e-230)*t^504 - (4.21995207946999e-230)*t^502 + (2.34279956582103e-228)*t^500 + (1.18236536505535e-227)*t^498 - (2.00373023099466e-226)*t^496 - (1.85041096454122e-225)*t^494 + (1.41545764362932e-224)*t^492 + (2.32622134939150e-223)*t^490 - (6.42094734195629e-223)*t^488 - (2.53118918236996e-221)*t^486 - (2.16979131393475e-221)*t^484 + (2.42443366020404e-219)*t^482 + (1.04174930525290e-218)*t^480 - (2.01350528204507e-217)*t^478 - (1.71184054671843e-216)*t^476 + (1.35636186652813e-215)*t^474 + (2.12860043778060e-214)*t^472 - (5.53311697476704e-214)*t^470 - (2.23429773485451e-212)*t^468 - (2.70131992906671e-212)*t^466 + (2.02398006471652e-210)*t^464 + (9.86293519736386e-210)*t^462 - (1.54693423649204e-208)*t^460 - (1.48944716174481e-207)*t^458 + (8.96988280798574e-207)*t^456 + (1.71565117384324e-205)*t^454 - (1.93537721487152e-205)*t^452 - (1.65377570749217e-203)*t^450 - (4.42527720836597e-203)*t^448 + (1.34521758614483e-201)*t^446 + (9.12522423106607e-201)*t^444 - (8.72517680017624e-200)*t^442 - (1.15790405045474e-198)*t^440 + (3.39796619667251e-198)*t^438 + (1.16855592922725e-196)*t^436 + (1.50140383764144e-196)*t^434 - (9.79999481102696e-195)*t^432 - (5.16542168452941e-194)*t^430 + (6.60914398966180e-193)*t^428 + (7.14625417195224e-192)*t^426 - (2.94662901073562e-191)*t^424 - (7.40001753854452e-190)*t^422 - (4.02653300110454e-190)*t^420 + (6.23541509832971e-188)*t^418 + (2.86133617059181e-187)*t^416 - (4.19007873935658e-186)*t^414 - (4.14821819474780e-185)*t^412 + (1.87368736329638e-184)*t^410 + (4.28497978942423e-183)*t^408 + (1.79404893855417e-183)*t^406 - (3.53167241254306e-181)*t^404 - (1.61355716223539e-180)*t^402 + (2.27845935056541e-179)*t^400 + (2.29328000406610e-178)*t^398 - (9.28126627495796e-178)*t^396 - (2.28378338421707e-176)*t^394 - (1.99548570572481e-176)*t^392 + (1.78745730849799e-174)*t^390 + (9.21889443396416e-174)*t^388 - (1.06157296225735e-172)*t^386 - (1.20102873639991e-171)*t^384 + (3.42410998722882e-171)*t^382 + (1.11378974244796e-169)*t^380 + (2.06073894850974e-169)*t^378 - (8.00611478373987e-168)*t^376 - (5.11662566657294e-167)*t^374 + (4.12184383680456e-166)*t^372 + (5.84433718616101e-165)*t^370 - (6.85535438357458e-165)*t^368 - (4.88736891499788e-163)*t^366 - (1.61761402666175e-162)*t^364 + (3.09329746131842e-161)*t^362 + (2.62678673932463e-160)*t^360 - (1.22605025613388e-159)*t^358 - (2.57162608988101e-158)*t^356 - (2.06988345440967e-158)*t^354 + (1.87628771297588e-156)*t^352 + (1.00071120434062e-155)*t^350 - (9.76059343650251e-155)*t^348 - (1.19900448933702e-153)*t^346 + (1.94396701275439e-153)*t^344 + (9.90594303724481e-152)*t^342 + (3.04799047186783e-151)*t^340 - (6.01490316489328e-150)*t^338 - (5.02003437127604e-149)*t^336 + (2.16583955197736e-148)*t^334 + (4.70935374892897e-147)*t^332 + (5.70455387627475e-147)*t^330 - (3.19834820907442e-145)*t^328 - (1.89682317461207e-144)*t^326 + (1.45624395543226e-143)*t^324 + (2.05673936991548e-142)*t^322 - (9.89418985555760e-143)*t^320 - (1.53306901738260e-140)*t^318 - (6.45327971195713e-140)*t^316 + (7.98793326998763e-139)*t^314 + (8.36920180362767e-138)*t^312 - (1.76331832157345e-137)*t^310 - (6.78349004149490e-136)*t^308 - (1.95334862873365e-135)*t^306 + (3.86925036639608e-134)*t^304 + (3.21025309383472e-133)*t^302 - (1.19176892377324e-132)*t^300 - (2.81391549142284e-131)*t^298 - (5.10257998912639e-131)*t^296 + (1.71309420742354e-129)*t^294 + (1.17354120354333e-128)*t^292 - (6.21141010526743e-128)*t^290 - (1.10670973916732e-126)*t^288 - (1.05971677063767e-126)*t^286 + (7.06484818482321e-125)*t^284 + (4.13424750046422e-124)*t^282 - (2.80629456697622e-123)*t^280 - (4.16317258727000e-122)*t^278 - (1.23216434176434e-122)*t^276 + (2.74584555935240e-120)*t^274 + (1.41973278995481e-119)*t^272 - (1.14678177284777e-118)*t^270 - (1.50819569199232e-117)*t^268 + (2.55400182649046e-118)*t^266 + (1.01347429074936e-115)*t^264 + (4.80491222950244e-115)*t^262 - (4.32371776232156e-114)*t^260 - (5.28849717815272e-113)*t^258 + (2.27693306456462e-113)*t^256 + (3.56960317196899e-111)*t^254 + (1.61665947134216e-110)*t^252 - (1.51902689605966e-109)*t^250 - (1.80067430737991e-108)*t^248 + (8.70136702162514e-109)*t^246 + (1.20297714163263e-106)*t^244 + (5.43177653693489e-106)*t^242 - (4.99343241343659e-105)*t^240 - (5.96078738372008e-104)*t^238 + (1.97967788296507e-104)*t^236 + (3.88200953421384e-102)*t^234 + (1.82073759363030e-101)*t^232 - (1.53542398747617e-100)*t^230 - (1.91707585848175e-99)*t^228 - (1.49860832151572e-101)*t^226 + (1.19831097337376e-97)*t^224 + (6.05371003979069e-97)*t^222 - (4.39468309554980e-96)*t^220 - (5.97569363065641e-95)*t^218 - (3.07600965426092e-95)*t^216 + (3.52824700717218e-93)*t^214 + (1.97908394967189e-92)*t^212 - (1.15763428322344e-91)*t^210 - (1.79829543027609e-90)*t^208 - (2.09745289596768e-90)*t^206 + (9.86060017508957e-89)*t^204 + (6.30069283107976e-88)*t^202 - (2.74169873045556e-87)*t^200 - (5.19803301632630e-86)*t^198 - (1.01206025784749e-85)*t^196 + (2.59617447378106e-84)*t^194 + (1.93558486656707e-83)*t^192 - (5.53501208974778e-83)*t^190 - (1.43420010943522e-81)*t^188 - (4.09461172762944e-81)*t^186 + (6.36509046085239e-80)*t^184 + (5.69055113252898e-79)*t^182 - (8.04965650878128e-79)*t^180 - (3.74855971867182e-77)*t^178 - (1.46599026955199e-76)*t^176 + (1.42543997751848e-75)*t^174 + (1.58902797116277e-74)*t^172 - (2.62489258413788e-76)*t^170 - (9.19102131578099e-73)*t^168 - (4.75324802917076e-72)*t^166 + (2.81044023693505e-71)*t^164 + (4.18287372332159e-70)*t^162 + (5.70616635203883e-70)*t^160 - (2.08522928611339e-68)*t^158 - (1.41054754776781e-67)*t^156 + (4.45479682120252e-67)*t^154 + (1.02918449613507e-65)*t^152 + (2.86644182809748e-65)*t^150 - (4.28250313796299e-64)*t^148 - (3.84603840802784e-63)*t^146 + (3.78615625925022e-63)*t^144 + (2.34091657841571e-61)*t^142 + (1.01713999310704e-60)*t^140 - (7.63184776334026e-60)*t^138 - (9.62744041717348e-59)*t^136 - (8.54107204676561e-59)*t^134 + (4.84095542579751e-57)*t^132 + (3.01539692161919e-56)*t^130 - (1.05765283991339e-55)*t^128 - (2.20054536092525e-54)*t^126 - (5.85358114395558e-54)*t^124 + (8.83810757785709e-53)*t^122 + (7.82854907008966e-52)*t^120 - (6.28897399305285e-52)*t^118 - (4.53968191068518e-50)*t^116 - (2.06293746364900e-49)*t^114 + (1.33493525100854e-48)*t^112 + (1.80576228106203e-47)*t^110 + (2.46657181516943e-47)*t^108 - (8.26146706628563e-46)*t^106 - (5.68077692677779e-45)*t^104 + (1.34065328846791e-44)*t^102 + (3.69478534922968e-43)*t^100 + (1.25804025915553e-42)*t^98 - (1.26157134085004e-41)*t^96 - (1.32468726696368e-40)*t^94 - (4.87303661355537e-41)*t^92 + (6.59564464633004e-39)*t^90 + (3.75640406923822e-38)*t^88 - (1.39510441286696e-37)*t^86 - (2.66756395414186e-36)*t^84 - (7.05839088128903e-36)*t^82 + (9.83376999392302e-35)*t^80 + (8.81705184249319e-34)*t^78 - (2.83887444968747e-34)*t^76 - (4.59889561018678e-32)*t^74 - (2.30638762214521e-31)*t^72 + (1.07582283928725e-30)*t^70 + (1.72493985594525e-29)*t^68 + (3.83931229624595e-29)*t^66 - (6.50736640117293e-28)*t^64 - (5.36721771487742e-27)*t^62 + (3.41267955815069e-27)*t^60 + (2.81529813940515e-25)*t^58 + (1.33589286904800e-24)*t^56 - (6.57741862760556e-24)*t^54 - (9.99553875007034e-23)*t^52 - (2.16323234029423e-22)*t^50 + (3.65648170468036e-21)*t^48 + (2.99463114086338e-20)*t^46 - (1.43456027962158e-20)*t^44 - (1.50259360417679e-18)*t^42 - (7.38532998606367e-18)*t^40 + (3.12932430209616e-17)*t^38 + (5.16337159695730e-16)*t^36 + (1.31981175149323e-15)*t^34 - (1.70149207922661e-14)*t^32 - (1.54180486809492e-13)*t^30 - (4.90154200583368e-14)*t^28 + (6.91855972936529e-12)*t^26 + (4.05550098204265e-11)*t^24 - (9.79296456629790e-11)*t^22 - (2.47086878306878e-9)*t^20 - (9.05444223985891e-9)*t^18 + (6.63005952380953e-8)*t^16 + (7.94682539682540e-7)*t^14 + (1.28333333333333e-6)*t^12 - 0.0000303333333333333*t^10 - 0.000230000000000000*t^8 + 0.000133333333333333*t^6 + 0.0120000000000000*t^4 + 0.0800000000000000*t^2 + 0.200000000000000
|